Trigonometric Substitution for Beginners: A Step-by-Step Guide
Trigonometric substitution is an integration technique that helps solve integrals involving expressions of the form \( a^2x^2 + b^2 \), \( a^2x^2 – b^2 \), and \( b^2 – a^2x^2 \). It transforms the expressions into trigonometric functions, which can be integrated using the techniques covered in my article How to Integrate Products of Trigonometric Functions: Techniques and Tricks. This guide on trigonometric substitution for beginners offers a step-by-step approach to learning trigonometric substitution.
The following infographic illustrates the concepts covered in this article.
Understanding Trigonometric Substitution
Trigonometric substitution is useful for integrals containing expressions of the form:
$$ \sqrt{b^2 – a^2x^2} \Rightarrow x = \frac{b}{a}\sin\theta $$
$$ \sqrt{a^2x^2 + b^2} \Rightarrow x = \frac{b}{a}\tan\theta $$
$$ \sqrt{a^2x^2 – b^2} \Rightarrow x = \frac{b}{a}\sec\theta. $$
Each substitution transforms the integral into a trigonometric integral, allowing us to integrate using trigonometric identities.
How to Solve an Integral Using Trigonometric Substitution
Step 1: Choosing the Proper Trigonometric Substitution
Choose the appropriate substitution based on the expression that appears in the integral.
Step 2: Making the Substitution
Substitute into the integral using the procedure discussed in The Ultimate Step-by-Step Guide to Solving Integrals Using Substitution.
Step 3: Simplifying the Integral
Use trigonometric identities to simplify the integrand as much as possible.
Step 4: Solving the Integral
Integrate the resulting trigonometric integral.
Step 5: Converting Back to x
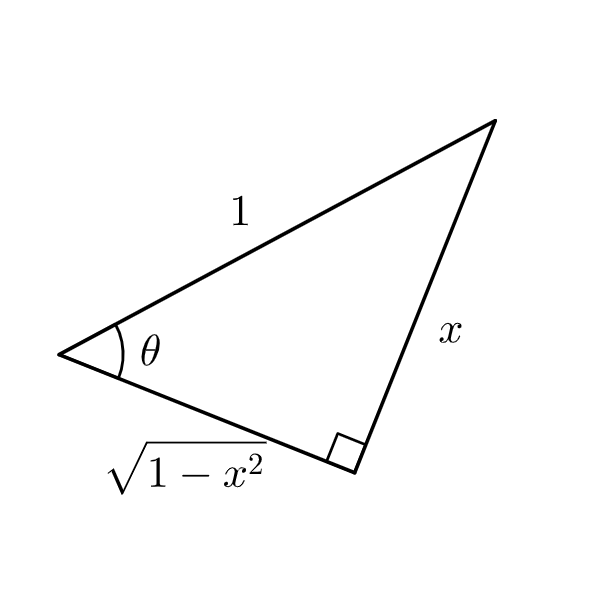
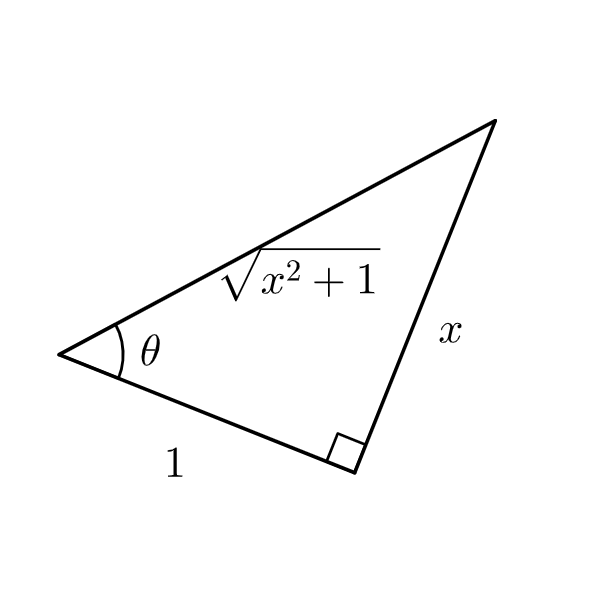
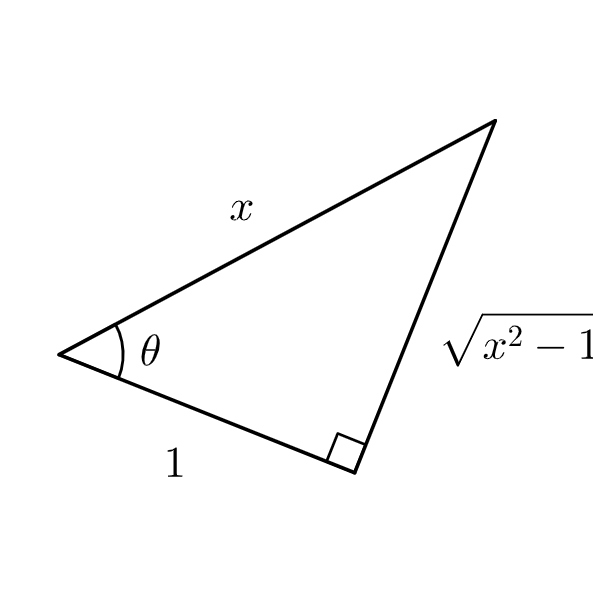
Use a right triangle to express \( \theta \) in terms of x.
Worked Out Examples
For each case, we will work through an indefinite integral and a definite integral.
Case 1: \( \sqrt{b^2 – a^2x^2} \Rightarrow x = \frac{b}{a}\sin\theta \)
Example 1: Evaluate:
(a) \( \int \frac{x^2}{\sqrt{1 – x^2}} dx \)
(b) \( \int_0^1 \frac{x^2}{\sqrt{1 – x^2}} dx \).
Solution: (a) \( \int \frac{x^2}{\sqrt{1 – x^2}} dx \)
Let \( x = \sin{\theta} \), then \( dx = \cos{\theta} d\theta \). Substituting into the integral, we get
$$ \int \frac{\sin^2{\theta}}{\sqrt{1 – sin^2{\theta}}}\cos{\theta} d\theta. $$
Applying the Pythagorean identity gives
$$ \int \frac{\sin^2{\theta}}{\sqrt{cos^2{\theta}}}\cos{\theta} d\theta. $$
Evaluating the square root, we obtain
$$ \int \frac{\sin^2{\theta}}{\cos{\theta}}\cos{\theta} d\theta. $$
This is equivalent to
$$ \int \sin^2{\theta} d\theta. $$
Applying the power-reducing identity gives
$$ \int \frac{1}{2} – \frac{1}{2}\cos{2\theta} d\theta. $$
Integrating we obtain
$$\frac{1}{2}\theta – \frac{1}{4}\sin{2\theta} + C. $$
Now we apply the double-angle identity for sine to get
$$ \frac{1}{2}\theta – \frac{1}{2}\sin{\theta}\cos{\theta} + C. $$
Shown below is the right triangle for our substitution.
Using the triangle to convert everything back into terms of x, we arrive at a final answer of
$$ \frac{1}{2}\arcsin{\theta} – \frac{1}{2}x\sqrt{1 – x^2} + C. $$
(b) \( \int_0^1 \frac{x^2}{\sqrt{1 – x^2}} dx \).
Let \( x = \sin{\theta} \), then \( dx = \cos{\theta} ol\theta \). By substituting the limits into the substitution and solving the resulting trigonometric equations, the new limits are \( 0 \Rightarrow 0 \) and \( 1 \Rightarrow \frac{\pi}{2} \). Substituting into the integral, we get
$$ \int_0^{\frac{\pi}{2}} \frac{\sin^2{\theta}}{\sqrt{1 – sin^2{\theta}}}\cos{\theta} d\theta. $$
Applying the Pythagorean Identity, we obtain
$$ \int_0^{\frac{\pi}{2}} \frac{\sin^2{\theta}}{\sqrt{cos^2{\theta}}}\cos{\theta} d\theta. $$
Computing the square root gives
$$ \int_0^{\frac{\pi}{2}} \frac{\sin^2{\theta}}{|\cos{\theta}|}\cos{\theta} d\theta. $$
Cosine is positive over the interval of integration, so we drop the absolute value bars to get
$$ \int_0^{\frac{\pi}{2}} \frac{\sin^2{\theta}}{\cos{\theta}}\cos{\theta} d\theta. $$
This is equivalent to
$$ \int_0^{\frac{\pi}{2}} \sin^2{\theta} d\theta. $$
Applying the power-reducing identity gives
$$ \int_0^{\frac{\pi}{2}} \frac{1}{2} – \frac{1}{2}\cos{2\theta} d\theta. $$
Integrating we get
$$ (\frac{1}{2}\theta – \frac{1}{4}\sin{2\theta})|_0^{\frac{\pi}{2}}. $$
By the Fundamental Theorem of Calculus, this is
$$ \frac{1}{2}\frac{\pi}{2} – \frac{1}{4}\sin{2\frac{\pi}{2}} – \frac{1}{2}0 + \frac{1}{4}\sin{2(0)}. $$
Multiplying we get
$$ \frac{\pi}{4} – \frac{1}{4}\sin{\pi} – 0 + \frac{1}{4}\sin{0}. $$
Evaluating the sine functions, we obtain
$$ \frac{\pi}{4} – \frac{1}{4}0 – 0 + \frac{1}{4}0. $$
Multiplying gives
$$ \frac{\pi}{4} – 0 – 0 + 0. $$
Simplifying, we arrive at a final answer of
$$ \frac{\pi}{4}. $$
Case 2: \( \sqrt{a^2x^2 + b^2} \Rightarrow x = \frac{b}{a}\tan\theta \)
Example 2: Evaluate:
(a) \( \int \frac{1}{\sqrt{x^2 + 1}} dx \)
(b) \( \int_0^1 \frac{1}{\sqrt{x^2 + 1}} dx \)
Solution: (a) \( \int \frac{1}{\sqrt{x^2 + 1}} dx \)
Let \( x = \tan{\theta} \), then \( dx = \sec^2{\theta} d\theta \). Substituting into the integral, we get
$$ \int \frac{1}{\sqrt{tan^2{\theta} + 1}}\sec^2{\theta} d\theta. $$
Applying the Pythagorean identity, we obtain
$$ \int \frac{1}{\sqrt{sec^2{\theta}}}\sec^2{\theta} d\theta. $$
Taking the square root gives
$$ \int \frac{1}{\sec{\theta}}\sec^2{\theta} d\theta. $$
This is equivalent to
$$ \int \sec{\theta} d\theta. $$
Multiplying the numerator and denominator by \( \sec{\theta} + \tan{\theta} \) we get
$$ \int \frac{\sec{\theta}(\sec{\theta} + \tan{\theta})}{\sec{\theta} + \tan{\theta}} d\theta. $$
Distributing \( \sec{\theta} \) we obtain
$$ \int \frac{\sec^2{\theta} + \sec{\theta}\tan{\theta}}{\sec{\theta} + \tan{\theta}} d\theta. $$
Let \( u = \sec{\theta} + \tan{\theta} \), then \( du = \sec^2{\theta} + \sec{\theta}\tan{\theta} d\theta \). Substituting into the integral, we get
$$ \int \frac{1}{u} du. $$
Integrating gives
$$ \ln{|u|} + C. $$
Back substituting, we obtain
$$ \ln{|\sec{\theta} + \tan{\theta}|} + C. $$
Shown below is the right triangle for our substitution.
Using the triangle to convert everything back into terms of x, we arrive at a final answer of
$$ \ln{|x + \sqrt{x^2 + 1}|} + C. $$
(b) \( \int_0^1 \frac{1}{\sqrt{x^2 + 1}} dx \).
Let \( x = \tan{\theta} \), then \( dx = \sec^2{\theta} d\theta \). By substituting the limits into the substitution and solving the resulting trigonometric equations, the new limits are \( 0 \Rightarrow 0 \) and \( 1 \Rightarrow \frac{\pi}{4} \). Substituting into the integral, we get
$$ \int_0^{\frac{\pi}{4}} \frac{1}{\sqrt{tan^2{\theta} + 1}}\sec^2{\theta} d\theta. $$
Applying the Pythagorean identity, we obtain
$$ \int_0^{\frac{\pi}{4}} \frac{1}{\sqrt{sec^2{\theta}}}\sec^2{\theta} d\theta. $$
Taking the square root gives
$$ \int_0^{\frac{\pi}{4}} \frac{1}{|\sec{\theta}|}\sec^2{\theta} d\theta. $$
Since secant is positive over the interval of integration, we drop the absolute value bars to get
$$ \int_0^{\frac{\pi}{4}} \frac{1}{\sec{\theta}}\sec^2{\theta} d\theta. $$
This simplifies to
$$ \int_0^{\frac{\pi}{4}} \sec{\theta} d\theta. $$
This is equivalent to
$$ \int_0^{\frac{\pi}{4}} \frac{\sec{\theta}(\sec{\theta} + \tan{\theta})}{\sec{\theta} + \tan{\theta}} d\theta. $$
Distributing \( \sec{\theta} \) we get
$$ \int_0^{\frac{\pi}{4}} \frac{\sec^2{\theta} + \sec{\theta}\tan{\theta}}{\sec{\theta} + \tan{\theta}} d\theta. $$
Let \( u = \sec{\theta} + \tan{\theta} \), then \( du = \sec^2{\theta} + \sec{\theta}\tan{\theta} d\theta \). The new limits are \( 0 \Rightarrow 1 \) and \( \frac{\pi}{4} \Rightarrow 1 + \sqrt{2} \). Substituting into the integral, we get
$$ \int_1^{1+ \sqrt{2}} \frac{1}{u} du. $$
Integrating gives
$$ \ln{|u|}|_1^{1+ \sqrt{2}}. $$
Applying the Fundamental Theorem of Calculus, we obtain
$$ \ln{|1 + \sqrt{2}|} – \ln{|1|}. $$
The argument of each logarithm is non-negative, so we can drop the absolute value bars to get
$$ \ln{(1 + \sqrt{2})} – \ln{1}. $$
\( \ln{1} =0 \), so we have
$$ \ln{(1 + \sqrt{2})} – 0. $$
Subtracting gives a final answer of
$$ \ln{(1 + \sqrt{2})}. $$
Case 3: \( \sqrt{a^2x^2 – b^2} \Rightarrow x = \frac{b}{a}\sec\theta \)
Example 3: Evaluate:
(a) \( \int \frac{1}{\sqrt{x^2 – 1}} dx \)
(b) \( \int_1^2 \frac{1}{\sqrt{x^2 – 1}} dx \)
Solution: (a) \( \int \frac{1}{\sqrt{x^2 – 1}} dx \)
Let \( x = \sec{\theta} \), then \( dx = \sec{\theta}\tan{\theta} d\theta \). Substituting into the integral, we get
$$ \int \frac{1}{\sqrt{sec^2{\theta} – 1}}\sec{\theta}\tan{\theta} d\theta. $$
Applying the Pythagorean identity, we obtain
$$ \int \frac{1}{\sqrt{tan^2{\theta}}}\sec{\theta}\tan{\theta} d\theta. $$
Taking the square root gives
$$ \int \frac{1}{\tan{\theta}}\sec{\theta}\tan{\theta} d\theta. $$
This simplifies to
$$ \int \sec{\theta} d\theta, $$
which is equivalent to
$$ \int \frac{\sec{\theta}(\sec{\theta} + \tan{\theta})}{\sec{\theta} + \tan{\theta}} d\theta. $$
Distributing \( \sec{\theta} \) gives
$$ \int \frac{\sec^2{\theta} + \sec{\theta}\tan{\theta}}{\sec{\theta} + \tan{\theta}} d\theta. $$
Let \( u = \sec{\theta} + \tan{\theta} \), then \( du = \sec^2{\theta} + \sec{\theta}\tan{\theta} d\theta \). Substituting into the integral, we get
$$ \int \frac{1}{u} du. $$
Integrating we obtain
$$ \ln{|u|} + C. $$
Back substituting gives
$$ \ln{|\sec{\theta} + \tan{\theta}|} + C. $$
Shown below is the right triangle for our substitution.
Using the triangle to convert everything back into terms of x, we arrive at a final answer of
$$ \ln{|x + \sqrt{x^2 – 1}|} + C. $$
(b) \( \int_1^2 \frac{1}{\sqrt{x^2 – 1}} dx \)
Let \( x = \sec{\theta} \), then \( dx = \sec{\theta}\tan{\theta} d\theta \). By substituting the limits into the substitution and solving the resulting trigonometric equations, the new limits are \( 1 \Rightarrow 0 \) and \( 2 \Rightarrow \frac{\pi}{3} \). Substituting into the integral, we get
$$ \int_0^{\frac{\pi}{3}} \frac{1}{\sqrt{sec^2{\theta} – 1}}\sec{\theta}\tan{\theta} d\theta. $$
Applying the Pythagorean identity, we obtain
$$ \int_0^{\frac{\pi}{3}} \frac{1}{\sqrt{tan^2{\theta}}}\sec{\theta}\tan{\theta} d\theta. $$
Taking the square root gives
$$ \int_0^{\frac{\pi}{3}} \frac{1}{|\tan{\theta}|}\sec{\theta}\tan{\theta} d\theta. $$
Tangent is positive over the interval of integration, so we can drop the absolute value bars to get
$$ \int_0^{\frac{\pi}{3}} \frac{1}{\tan{\theta}}\sec{\theta}\tan{\theta} d\theta. $$
This simplifies to
$$ \int_0^{\frac{\pi}{3}} \sec{\theta} d\theta, $$
which is equivalent to
$$ \int_0^{\frac{\pi}{3}} \frac{\sec{\theta}(\sec{\theta} + \tan{\theta})}{\sec{\theta} + \tan{\theta}} d\theta. $$
Distributing \( \sec{\theta} \) gives
$$ \int_0^{\frac{\pi}{3}} \frac{\sec^2{\theta} + \sec{\theta}\tan{\theta}}{\sec{\theta} + \tan{\theta}} d\theta. $$
Let \( u = \sec{\theta} + \tan{\theta} \), then \( du = \sec^2{\theta} + \sec{\theta}\tan{\theta} d\theta \). The new limits are \( 0 \Rightarrow 1 \) and \( \frac{\pi}{3} \Rightarrow 2 + \sqrt{3} \). Substituting into the integral, we get
$$ \int_1^{2 + \sqrt{3}} \frac{1}{u} du. $$
Integrating gives
$$ \ln{|u|}|_1^{2 + \sqrt{3}}. $$
By the Fundamental Theorem of Calculus, this is
$$ \ln{|2 + \sqrt{3}|} – \ln{|1|}.$$
The argument of each logarithm is positive, so we can drop the absolute value bars to obtain
$$ \ln{(2 + \sqrt{3})} – \ln{1}.$$
Evaluating the second logarithm gives
$$ \ln{(2 + \sqrt{3})} – 0.$$
Subtracting, we arrive at a final answer of
$$\ln{(2 + \sqrt{3})}. $$
The last example shows that another method, like integration by parts, must sometimes be used before we can use a trigonometric substitution. For help with integration by parts, see my article Integration by Parts Explained with Examples: A Step-by-Step Guide.
Example 4: Using example 3 as a lemma, evaluate \( \int \text{arcsec}(x) dx \).
Solution: Choose \( u = \text{arcsec}(x) \) and \( dv = dx \), then \( du = \frac{1}{x\sqrt{x^2 – 1}}dx \) and \( v = x \). Applying the integration by parts formula then gives
$$ x \text{arcsec}(x) – \int \frac{1}{\sqrt{x^2 – 1}} dx.$$
Integrating we get
$$ x \text{arcsec}(x) – (\ln{|x + \sqrt{x^2 – 1}|} + C).$$
Distributing the minus sign, we arrive at a final answer of
$$ x \text{arcsec}(x) – \ln{|x + \sqrt{x^2 – 1}|} + C.$$
Conclusion
Trigonometric substitution is an important technique in integral calculus. These more specialized integrals can be evaluated by recognizing the appropriate quadratics and corresponding substitutions, as covered in this guide on trigonometric substitution for beginners. Practice this method to become more proficient in solving integrals using trigonometric substitution.
Further Reading
The Ultimate Guide on How to Solve Integrals by Completing the Square – Now that you know how to use trigonometric substitution, you can use it along with completing the square to solve integrals of the form \( \int \frac{Ax + B}{(ax^2 + bx + c)^n} dx \).
