Partial fraction decomposition is one of the most used techniques for solving integrals involving rational functions. This method allows us to express a rational function as a sum of simpler fractions that can be integrated via other methods, such as substitution and completing the square. This tutorial will provide partial fraction decomposition integration problems with solutions.

The partial fraction decomposition problems given here will lead to systems that are best solved using techniques from linear algebra. Please see How to Solve a System of Equations Using Gaussian Elimination: A Step-by-Step Guide to learn one of these techniques.

This article is part of a three-part series on integrals of rational functions. To learn this topic visually, please refer to the Integrating Rational Functions Infographic.

Partial Fraction Decomposition

Partial fraction decomposition is a method for expressing a rational function as a sum of simpler fractions. This is useful in integration because then each fraction can be integrated separately. Specifically, this technique is useful when integrating proper rational functions where the degree of the numerator is less than the degree of the denominator, and the denominator consists of a reducible polynomial.

Steps for Integrating via Partial Fraction Decomposition

Step 1: Check that the Rational Function is Proper

To use partial fraction decomposition, the degree of the numerator must be less than that of the denominator. If it is not, you must first use polynomial long division. Please check out my article How to Integrate Using Polynomial Long Division with Examples to see how this is done.

Step 2: Factor the Denominator

Factor the denominator into linear or irreducible quadratic terms. If the denominator cannot be factored, skip to step 4.

Step 3: Find the Partial Fraction Decomposition

For help with this process, please refer to A Comprehensive Beginner’s Guide to Partial Fraction Decomposition, which explains how to find the partial fraction decomposition for a rational function.

Step 4: Integrate Each Term

Once the function is rewritten as a sum of simpler fractions, integrate each term separately using techniques discussed in the articles Basic Integration Problems for Beginners, The Ultimate Step-by-Step Guide to Solving Integrals Using Substitution, and The Ultimate Guide on How to Solve Integrals by Completing the Square.

Worked Out Examples

Example 1: Evaluate \( \int \frac{50}{x^2(x^2 + 6x + 10)} dx \).
Solution: Setting up the partial fraction decomposition, we get

$$\frac{50}{x^2(x^2 + 6x + 10)} = \frac{A}{x} + \frac{B}{x^2} + \frac{Cx + D}{x^2 + 6x + 10}.$$

Next, multiplying both sides by \( x^2(x^2 + 6x + 10) \) gives

$$50 = Ax(x^2 + 6x + 10) + B(x^2 + 6x + 10) + (Cx + D)x^2.$$

By expanding the right-hand side of the equation, we obtain

$$50 = Ax^3 + 6Ax^2 + 10Ax + Bx^2 + 6Bx + 10B + Cx^3 + Dx^2.$$

Adding like terms, we find

$$50 = (A + C)x^3 + (6A+ B + D)x^2 + (10A + 6B)x + 10B.$$

Next, we equate coefficients to obtain the system of equations

$$\begin{aligned}
A + C &= 0 \\
6A + B + D &= 0 \\
10A + 6B &= 0 \\
10B &= 50
\end{aligned}.$$

The solution to this system is

$$A = -3, B = 5, C = 3, D = 13.$$

Thus,

$$\frac{50}{x^2(x^2 + 6x + 10)} = -\frac{3}{x} + \frac{5}{x^2} + \frac{3x + 13}{x^2 + 6x + 10}.$$

Our integral is then

$$\int -\frac{3}{x} + \frac{5}{x^2} + \frac{3x + 13}{x^2 + 6x + 10} dx = \int -\frac{3}{x} + \frac{5}{x^2} + \frac{3}{2}\frac{2x + 6}{x^2 + 6x + 10} + \frac{4}{x^2 + 6x + 10} dx.$$

Next, use linearity to split the integral into three integrals as follows:

$$\int \frac{-3}{x} + \frac{5}{x^2} dx + \frac{3}{2} \int \frac{2x + 6}{x^2 + 6x + 10} dx + 4\int \frac{1}{x^2 + 6x + 10} dx.$$

Now, we complete the square in the third integral, which gives

$$\int \frac{-3}{x} + \frac{5}{x^2} dx + \frac{3}{2} \int \frac{2x + 6}{x^2 + 6x + 10} dx + 4\int \frac{1}{x^2 + 6x + 9 + 1} dx = \int \frac{-3}{x} + \frac{5}{x^2} dx + \frac{3}{2} \int \frac{2x + 6}{x^2 + 6x + 10} dx + 4\int \frac{1}{(x + 3)^2 + 1} dx.$$

In the second integral, let \( u = x^2 + 6x + 10 \), then \( du = (2x + 6)dx \). For the third integral, let \( v = x + 3 \), then \( dv = dx \). Substituting into the integrals, we have

$$\int \frac{-3}{x} + \frac{5}{x^2} dx + \frac{3}{2} \int \frac{1}{u} du + 4\int \frac{1}{v^2 + 1} dv = \int \frac{-3}{x} + 5x^{-2} dx + \frac{3}{2} \int \frac{1}{u} du + 4\int \frac{1}{v^2 + 1} = -3\ln{|x|} – 5x^{-1} + \frac{3}{2}\ln{|u|} + 4\arctan{v} + C = -3\ln{|x|} – \frac{5}{x} + \frac{3}{2}\ln{|u|} + 4\arctan{v} + C.$$

Back substituting gives us

$$-3\ln{|x|} – \frac{5}{x} + \frac{3}{2}\ln{|x^2 + 6x + 10|} + 4\arctan{(x + 3)} + C.$$

Example 2: Evaluate \( \int \frac{100}{x(x^2 + 6x + 10)^2} dx \).

Solution: Setting up the partial fraction decomposition, we get

$$\frac{100}{x(x^2 + 6x + 10)^2} = \frac{A}{x} + \frac{Bx + C}{x^2 + 6x + 10} + \frac{Dx + E}{(x^2 + 6x + 10)^2}.$$

Next, multiplying both sides by \( x(x^2 + 6x + 10)^2 \) gives

$$100 = A(x^2 + 6x + 10)^2 + (Bx+C)x(x^2 + 6x + 10) + (Dx + E)x.$$

By expanding the right-hand side of the equation, we obtain

$$100 = A(x^4 + 12x^3 + 56x^2 + 120x + 100 + (Bx + C)(x^3 + 6x^2 + 10x) + (Dx + E)x.$$

$$100 = Ax^4 + 12Ax^3 + 56Ax^2 + 120Ax + 100A + Bx^4 + 6Bx^3 + 10Bx^2 + Cx^3 + 6Cx^2 + 10Cx + Dx^2 + Ex.$$

Adding like terms, we find

$$100 = (A + B)x^4 + (12A + 6B + C)x^3 + (56A + 10B + 6C + D)x^2 + (120A + 10C + E)x + 100A.$$

Next, we equate coefficients to obtain the system of equations

$$\begin{aligned}
A + B &= 0 \\
12A + 6B + C &= 0 \\
56A + 10B + 6C + D &= 0 \\
120A + 10C + E &= 0 \\
100A = 100
\end{aligned}.$$

The solution to this system is

$$A = 1, B = -1, C = -6, D = -10, E = -60.$$

Thus,

$$\frac{100}{x(x^2 + 6x + 10)^2} = \frac{1}{x} – \frac{x + 6}{x^2 + 6x + 10} – \frac{10x + 60}{(x^2 + 6x + 10)^2}.$$

Our integral is then

$$\int \frac{1}{x} – \frac{x + 6}{x^2 + 6x + 10} – \frac{10x + 60}{(x^2 + 6x + 10)^2} dx = \int \frac{1}{x} – \frac{1}{2}\frac{2x + 6}{x^2 + 6x + 10} – \frac{3}{x^2 + 6x + 10} – 5\frac{2x + 6}{(x^2 + 6x + 10)^2} – \frac{30}{(x^2 + 6x + 10)^2} dx.$$

Next, use linearity to split the integral into four integrals as follows:

$$\int \frac{1}{x} dx – \int \frac{1}{2}\frac{2x + 6}{x^2 + 6x + 10} – 5\frac{2x + 6}{(x^2 + 6x + 10)^2} dx – 3\int \frac{1}{x^2 + 6x +10} dx – 30\int \frac{1}{(x^2 + 6x + 10)^2} dx.$$

Now, we complete the square in the third and fourth integrals, which gives

$$\int \frac{1}{x} dx – \int \frac{1}{2}\frac{2x + 6}{x^2 + 6x + 10} – 5\frac{2x + 6}{(x^2 + 6x + 10)^2} dx – 3\int \frac{1}{x^2 + 6x + 9 + 1} dx – 30\int \frac{1}{(x^2 + 6x + 9 + 1)^2} dx = \int \frac{1}{x} dx – \int \frac{1}{2}\frac{2x + 6}{x^2 + 6x + 10} – 5\frac{2x + 6}{(x^2 + 6x + 10)^2} dx – 3\int \frac{1}{(x + 3)^2 + 1} dx – 30\int \frac{1}{((x + 3)^2 + 1)^2} dx.$$

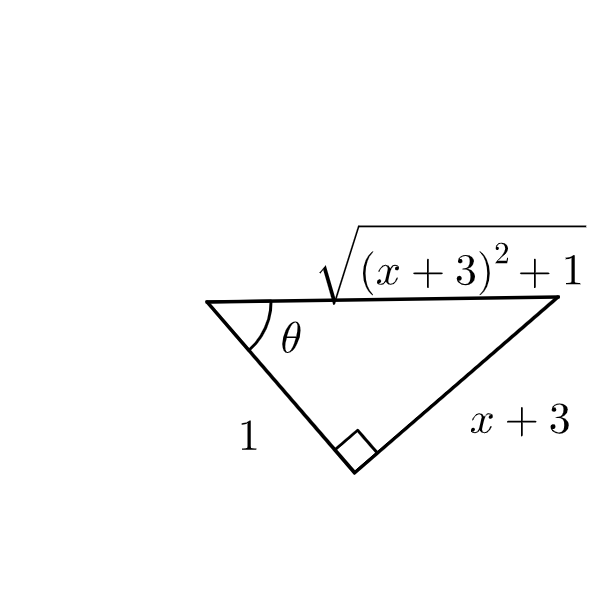
In the second integral, let \( u = x^2 + 6x + 10 \), then \( du = (2x + 6)dx \). For the third integral, let \( v = x + 3 \), then \( dv = dx \). In the fourth integral let \( x + 3 = \tan{\theta} \), then \( dx = \sec^2{\theta} d\theta \). Substituting into the integrals, we have

$$\int \frac{1}{x} dx – \int \frac{1}{2}\frac{1}{u} – 5\frac{1}{u^2} du – 3\int \frac{1}{v^2 + 1} dv – 30\int \frac{1}{(\tan^2{\theta} + 1)^2}\sec^2{\theta} d\theta = \int \frac{1}{x} dx – \int \frac{1}{2}\frac{1}{u} – 5\frac{1}{u^2} du – 3\int \frac{1}{v^2 + 1} dv – 30\int \frac{1}{(\sec^2{\theta})^2}\sec^2{\theta} d\theta = \int \frac{1}{x} dx – \int \frac{1}{2}\frac{1}{u} – 5\frac{1}{u^2} du – 3\int \frac{1}{v^2 + 1} dv – 30\int \frac{1}{\sec^2{\theta}} d\theta = \int \frac{1}{x} dx – \int \frac{1}{2}\frac{1}{u} – 5u^{-2} du – 3\int \frac{1}{v^2 + 1} dv – 30\int \cos^2{\theta} d\theta = \int \frac{1}{x} dx – \int \frac{1}{2}\frac{1}{u} – 5u^{-2} du – 3\int \frac{1}{v^2 + 1} dv – 15\int 1 + \cos{(2\theta)} d\theta = \ln{|x|} – \frac{1}{2}\ln{|u|} + 5u^{-1} – 3\arctan{v} – 15\theta – \frac{15}{2}\sin{(2\theta)} + C = \ln{|x|} – \frac{1}{2}\ln{|u|} + \frac{5}{u} – 3\arctan{v} – 15\theta – 15\sin{\theta}\cos{\theta} + C.$$

Trigonometric Substitution Tangent x Plus 3

Using the triangle and back substituting gives us

$$\ln{|x|} – \frac{1}{2}\ln{|x^2 + 6x + 10|} + \frac{5}{x^2 + 6x + 10} – 3\arctan{(x + 3)} – 15\arctan{(x + 3)} – \frac{15(x + 3)}{(x + 3)^2 + 1} + C = \ln{|x|} – \frac{1}{2}\ln{|x^2 + 6x + 10|} + \frac{5}{x^2 + 6x + 10} – 18\arctan{(x + 3)} – \frac{15(x + 3}{x^2 + 6x + 10} + C = \ln{|x|} – \frac{1}{2}\ln{|x^2 + 6x + 10|} – 18\arctan{(x + 3)} – \frac{15x + 40}{x^2 + 6x + 10} + C.$$

Conclusion

Partial fraction decomposition is a powerful method used to integrate rational functions. With it, along with polynomial long division and completing the square, you can, in theory, integrate any rational function.

Frequently Asked Questions

In theory, yes, but in practice, no. The reason for this is that not all polynomials, especially those of degree 5 or higher, have roots that can be expressed in terms of radicals. The branch of math called Galois Theory studies this phenomenon.

Founder

Joe Barnett is the founder of The Math Perimeter, driven by a passion for making mathematics education accessible, engaging, and approachable for all learners. With Bachelor of Science degrees in mathematics and physics, as well as a Master of Science in physics, Joe has a deep understanding of the subject and a strong commitment to effectively communicating advanced mathematical concepts. His experience as a graduate teaching assistant exposed him to the challenges students face in learning math, inspiring him to create a resource that breaks down concepts into intuitive, structured lessons. Living with a disability, Joe understands the importance of accessibility in education and is dedicated to ensuring that The Math Perimeter provides an inclusive learning experience. Through this platform, he aims to empower students to not just learn math, but to truly understand and appreciate the subject.