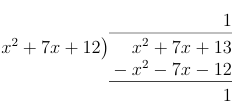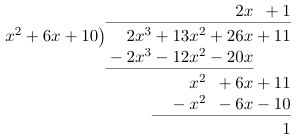How to Integrate Using Polynomial Long Division with Examples

When integrating a rational function where the degree of the numerator is greater than or equal to the degree of the denominator, polynomial long division becomes a valuable tool for simplifying the integral. In this guide, we’ll look at how to integrate using polynomial long division and work through a step-by-step example to solidify your understanding.

This article is part of a three-part series on integrals of rational functions. The following infographic illustrates this topic.

View Full Size Infographic

Polynomial Long Division

Before integrating, let’s review polynomial long division. This process allows us to rewrite an improper rational function as a sum of a polynomial and a proper fraction, making integration possible with other methods like partial fraction decomposition or completing the square, and maybe even simpler methods.

A proper rational function has a numerator with a degree less than the degree of the denominator. In comparison, an improper rational function has a numerator with a degree greater than or equal to the degree of the denominator. When faced with the latter, polynomial long division helps us write the rational function as the sum of a polynomial and a proper rational function.

Steps to Integrating Using Polynomial Long Division

Step 1: Check That the Rational Function is Improper

Check to make sure the degree of the numerator is greater than or equal to the degree of the denominator. If not, try a different method.

Step 2: Use Polynomial Long Division to Rewrite the Rational Function

We demonstrate this process by rewriting $ \frac{x^2 + 7x + 13}{x^2 + 7x + 12} $.

We first perform polynomial long division:

We now rewrite our function according to the word equation

$$\frac{dividend}{divisor} = quotient + \frac{remainder}{divisor}.$$

In our case, this gives

$$\frac{x^2 + 7x + 13}{x^2 + 7x + 12} = 1 + \frac{1}{x^2 + 7x + 12}.$$

Step 3: Integrate Term-by-Term

The polynomial function can be integrated using the methods covered in the article Basic Integration Problems for Beginners. These methods may also be used to integrate the rational function, but in all likelihood, you will need the techniques covered in The Ultimate Step-by-Step Guide to Solving Integrals Using Substitution or The Ultimate Guide on How to Solve Integrals by Completing the Square to solve it.

Partial fraction decomposition may also be needed. To learn how to find the partial fraction decomposition of a rational function, please check out A Comprehensive Beginner’s Guide to Partial Fraction Decomposition. The article Partial Fraction Decomposition Integration Problems with Solutions: A Complete Tutorial shows how partial fraction decomposition is used to integrate rational functions.

Worked Out Example

We now give an example.

Example 1: Evaluate:
(a) $ \int \frac{2x^3 + 13x^2 + 26x + 11}{x^2 + 6x + 10}dx $
(b) $ \int \frac{x^2 + 7x + 13}{x^2 + 7x + 12}dx $

Watch the video solution: A Beginner’s Guide to Polynomial Long Division in Integration

Solution: (a) $ \int \frac{2x^3 + 13x^2 + 26x + 11}{x^2 + 6x + 10}dx $

We first perform polynomial long division: as follows:

Rewriting the fraction then gives

$$\int 2x + 1 + \frac{1}{x^2 + 6x + 10}dx.$$

By linearity, this is

$$\int 2x + 1 dx + \int \frac{1}{x^2 + 6x + 10}dx.$$

We now complete the square in the denominator of the second integral. Begin by writing 10 as 9 + 1 to get

$$\int 2x + 1 dx + \int \frac{1}{x^2 + 6x + 9 + 1}dx. $$

This is equivalent to

$$\int 2x + 1 dx + \int \frac{1}{(x + 3)^2 + 1}dx. $$

Let $ u = x + 3 $, the $ du = dx $. Substituting into the second integral, we get

$$\int 2x + 1 dx + \int \frac{1}{u^2 + 1}du.$$

Integrating gives

$$x^2 + x + \arctan{u} + C.$$

Back substituting we arrive at a final answer of

$$x^2 + x + \arctan{(x + 3)} + C.$$

(b) $ \int \frac{x^2 + 7x + 13}{x^2 + 7x + 12}dx $

We first perform polynomial long division: as follows:

Rewriting the fraction then gives

$$\int 1 + \frac{1}{x^2 + 7x + 12}dx.$$

Factoring the denominator, we obtain

$$\int 1 + \frac{1}{(x + 3)(x + 4)}dx.$$

We now need to find the partial fraction decomposition of $ \frac{1}{(x + 3)(x + 4)} $. Setting up the partial fraction decomposition, we get

$$\frac{1}{(x + 3)(x + 4)} = \frac{A}{x + 3} + \frac{B}{x + 4}.$$

Next, multiplying both sides by $ (x + 3)(x + 4) $ gives

$$1 = A(x + 4) + B(x + 3).$$

Now we solve for the coefficients by choosing convenient values of x:

$$x = -3 \Rightarrow 1 = A$$

$$x = -4 \Rightarrow 1 = -B \Rightarrow -1 = B.$$

Thus,

$$\frac{1}{(x + 3)(x + 4)} = \frac{1}{x + 3} – \frac{1}{x + 4}.$$

Our integral is then

$$\int 1 + \frac{1}{x + 3} – \frac{1}{x + 4}dx.$$

Integrating gives

$$x + \ln{|x + 3|} – \ln{|x + 4|} + C.$$

Using logarithmic properties we arrive at a final answer of

$$x + \ln{|\frac{x + 3}{x + 4}|} + C.$$

Conclusion

Polynomial long division is an important tool in integration, especially when dealing with improper rational functions. This guide taught you how to integrate using polynomial long division. By mastering this technique, along with completing the square and partial fraction decomposition, you can, at least in theory, integrate any rational function.

Frequently Asked Questions

No, polynomial long division is only useful when the degree of the numerator is greater than or equal to the degree of the denominator. If the denominator is of a higher degree, other techniques like partial fraction decomposition, substitution, or completing the square are necessary.

Take The Next Step

Take your understanding of integral calculus beyond this article with Thinking in Integrals, a comprehensive guide designed to help you build a deeper understanding of integral calculus.

Learn More About the eBook

Support The Math Perimeter

If you enjoyed this article, please consider supporting The Math Perimeter on Buy Me a Coffee, so I can keep making more content like it.