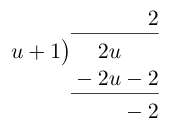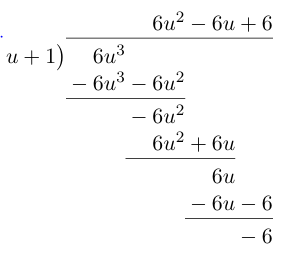Rationalizing substitution is a valuable tool when dealing with integrals involving roots. In this guide, we’ll cover what rationalizing substitution is, how to use it, and we will walk through step-by-step examples of rationalizing substitution in calculus.
What Is Rationalizing Substitution?
Rationalizing substitution is a technique for transforming integrals that involve roots into a rational function so that integration techniques like polynomial long division and partial fraction decomposition can be used.
Steps for Integrating Using Rationalizing Substitution
Step 1: Identify the Proper Substitution
Identify the substitution needed to transform the integrand into a rational function. In most cases this will be \( u = \sqrt[n]{f(x)} \) if only 1 root is present, or \( \sqrt[\gcd{(n_1, …, n_i)}]{f(x)} \) if multiple roots are present. In both cases \( f(x) \) is linear.
Step 2: Substitute into the integral
For help performing the substitution, please see The Ultimate Step-by-Step Guide to Solving Integrals Using Substitution.
Step 3: Integrate and Back Substitute
Now that the integrand is transformed into a rational function, it can be integrated using methods like polynomial long division, completing the square, and partial fraction decomposition, which are discussed in the articles How to Integrate Using Polynomial Long Division with Examples, Partial Fraction Decomposition Integration Problems with Solutions: A Complete Tutorial, and The Ultimate Guide on How to Solve Integrals by Completing the Square.
Worked Out Examples
Example 1: Evaluate \( \int \frac{1}{\sqrt{x} + 1} dx \).
Solution: Let \( u = \sqrt{x} \), which implies \( u^2 = x \), then \( 2udu = dx \). Substituting into the integral gives
$$\int \frac {2u}{u + 1} du.$$
We now perform polynomial long division:
Rewriting the fraction, the integral becomes
$$\int 2 – \frac{2}{u + 1} du = 2u – 2\ln{|u + 1|} + C = 2\sqrt{x} – 2\ln{|\sqrt{x} + 1|} + C.$$
Example 2: Evaluate \( \int \frac{1}{\sqrt[3]{x} + \sqrt{x}} dx \).
Solution: Let \( u = \sqrt[6]{x} \), which implies \( u^6 = x \), then \( 6u^5du = dx \). Substituting into the integral gives
$$\int \frac {6u^5}{u^3 + u^2} du = \int \frac {6u^5}{u^2(u + 1)} du = \int \frac {6u^3}{u + 1} du.$$
We now perform polynomial long division:
Rewriting the fraction, the integral becomes
$$\int 6u^2 – 6u + 6 – \frac{6}{u + 1} du = 2u^3 – 3u^2 + 6u – \ln{|u + 1|} + C = 2\sqrt{x} – 3\sqrt[3]{x} + 6\sqrt[6]{x} – \ln{|\sqrt[6]{x} + 1|} + C.$$
Conclusion
Rationalizing substitution is a method to transform integrals involving radicals into integrals of rational functions.