In this guide, you’ll find double and triple integrals explained with examples for general regions, written for beginners or those needing a refresher. Whether you’re working with regions in the plane or volumes bounded by curved surfaces, this guide will help you approach these kinds of problems.
Double and triple integrals are tools for calculating areas, volumes, and masses in two and three dimensions. When the region of integration is a simple rectangle or box, the setup is straightforward, but when you’re dealing with curves or surfaces as the boundaries, you need to be able to work with general regions.
In this article, we’ll focus on setting up and solving integrals over general regions using only Cartesian coordinates. We’ll start by discussing what general regions look like in both 2D and 3D. Then, we’ll walk through examples of double and triple integrals over these regions.
Before learning how to evaluate double and triple integrals over general regions, it is necessary to understand how to evaluate double and triple integrals over rectangular regions, so please be sure to read A Step-by-Step Beginner’s Tutorial for Double and Triple Integrals in Calculus.
General Regions in 2D and 3D
Before discussing double and triple integrals, it’s important to understand what we mean by a general region. In many introductory problems, you’re asked to integrate over simple rectangles or boxes. However, in more advanced problems, the region can be bounded by curves or surfaces. These are referred to as general regions, and they require more attention when setting up the integrals.
What Is a General Region?
A general region is any two- or three-dimensional area or volume that isn’t a perfect rectangle or box. It may be bounded by curves such as parabolas, circles, or other functions. It may even have boundaries that depend on several variables.
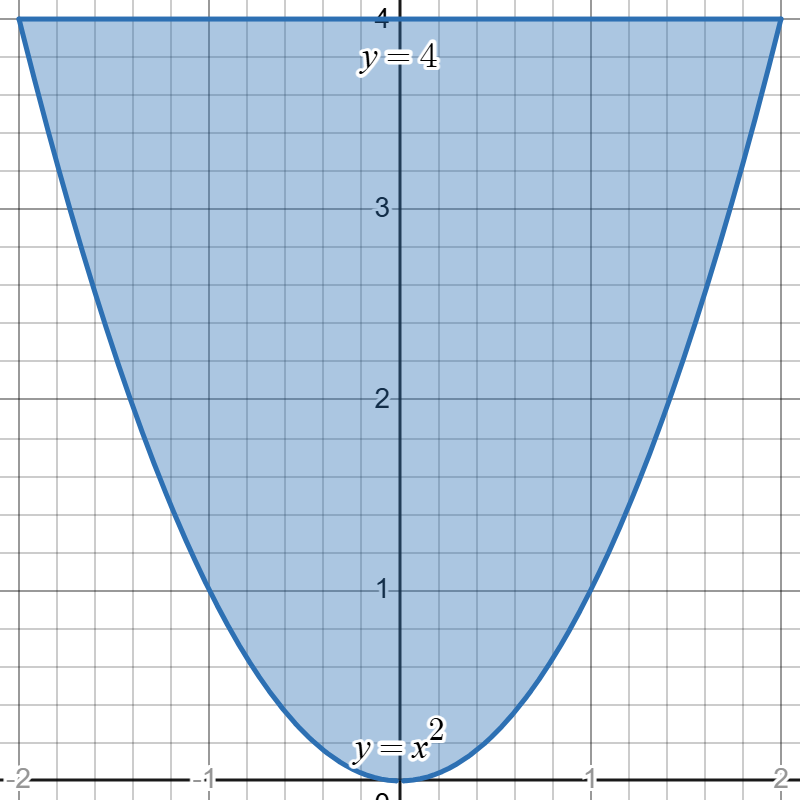
The region bounded by \( y = x^2 \) and \( y = 4 \) is a general region because the lower boundary is a curve, not a constant.
There are two ways to describe this region in Cartesian coordinates, they are:
$$\{ (x,y) | -2 \leq x \leq 2, x^2 \leq y \leq 4 \}$$
$$\{ (x,y) | -\sqrt{y} \leq x \leq \sqrt{y}, 0 \leq y \leq 4 \}.$$
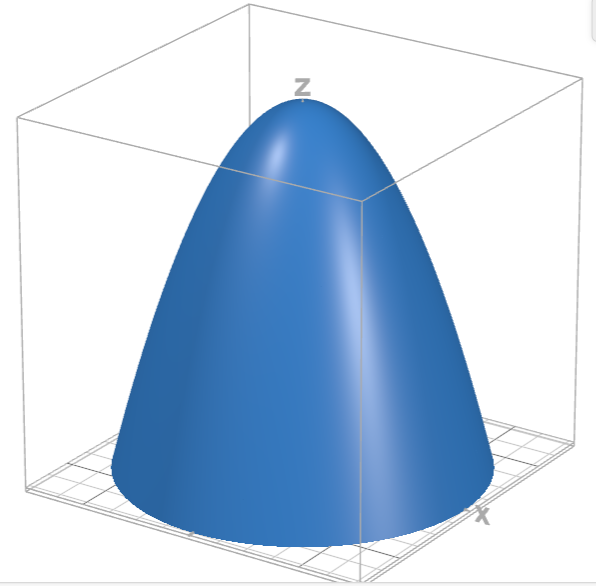
The solid bounded above by the paraboloid \( z = 9 – x^2 – y^2 \) and below by the \( xy \)-plane is a general region because the top surface is curved.
There are six ways to describe this region in Cartesian coordinates. One way is
$$\{ (x, y, z) | -\sqrt{9 – y^2 – z} \leq x \leq \sqrt{9 – y^2 – z}, -\sqrt{9-z} \leq y \leq \sqrt{9 – z}, 0 \leq 9 \}.$$
Double Integrals Over General Regions
When evaluating a double integral over a general region, the most important step is setting up the correct bounds. Once the limits are in place, the rest is just integration. That said, please refer to Basic Integration Problems for Beginners for a review of integration.
Examples
Example 1: Evaluate \( \int_{0}^{1} \int_{x^2}^{x+1} (3x + 2y)\,dy\,dx \).
Solution: The inner integral is with respect to y, so we treat \( x \) as a constant and integrate with respect to \( y \) to get
$$\int_{0}^{1} 3xy + y^2|_{x^2}^{x+1} dx = \int_{0}^{1} 3x(x + 1) + (x+1)^2 – 3x^3 – x^4 dx = -\int_{0}^{1} x^4 + 3x^3 – 4x^2 – 5x – 1dx.$$
Now, we evaluate the remaining integral to obtain
$$-\frac{1}{5}x^5 – \frac{3}{4}x^4 + \frac{4}{3}x^3 + \frac{5}{2}x^2 + x |_0^1 = \frac{233}{60}.$$
This next integral requires a substitution. Please check out The Ultimate Step-by-Step Guide to Solving Integrals Using Substitution to learn more about this method.
Example 2: Evaluate \( \int_{0}^{1} \int_{0}^{\sqrt{y}} x \sqrt{1 + x^2} dxdy \).
Solution: The Inner Integral is with respect to x, so we treat \( y \) as a constant and integrate with respect to \( x \). We begin with a substitution. Let \( u = 1 + x^2 \), then \( du = 2x dx \), which implies \( \frac{1}{2} du = x dx \). The new limits are \( 1 + 0^2 = 1 \) and \( 1 + \sqrt{y}^2 = 1 + y \). Substituting into the integral gives
$$\frac{1}{2} \int_{0}^{1} \int_{1}^{y + 1} \sqrt{u} dudy = \frac{1}{2} \int_{0}^{1} \int_{1}^{y + 1} u^{\frac{1}{2}} dudy = \frac{1}{3} \int_{0}^{1} u^{\frac{3}{2}}|_1^{y+1} dy = \frac{1}{3}\int_{0}^{1} (y+1)^{\frac{3}{2}} – 1 dy.$$
To evaluate the remaining integral, we begin by using linearity to get
$$\frac{1}{3} \int_{0}^{1} (y+1)^{\frac{3}{2}} dy – \frac{1}{3} \int_{0}^{1} dy.$$
The first integral can be evaluated with a substitution. Let \( u = y + 1 \), then \( du = dy \). The new limits are \( 0 + 1 = 1 \) and \( 1 + 1 = 2 \). Substituting into the first integral gives
$$\frac{1}{3} \int_{1}^{2} u^{\frac{3}{2}} dy – \frac{1}{3} \int_{0}^{1} dy = \frac{2}{15} u^{\frac{5}{2}}|_1^2 – \frac{1}{3} y|_0^1 = \frac{2}{15}\sqrt{32} – \frac{7}{15}.$$
Triple Integrals Over General Regions
As with double integrals, when evaluating a triple integral over a general region, the most important step is setting up the correct bounds. Once the limits are in place, the rest is just integration.
Examples
Example 3: Evaluate \( \int_0^1 \int_0^1 \int_0^1 x + y + z dxdydz \).
Solution: The inner integral is with respect to x, so we treat \( y \) and \( z \) as constants and integrate with respect to \( x \) to get
$$\int_0^1 \int_0^1 \frac{1}{2}x^2 + xy + xz|_0^1 dydz = \int_0^1 \int_0^1 \frac{1}{2} + y + z dydz.$$
We now integrate with respect to y while treating z as a constant. This gives
$$\int_0^1 \frac{1}{2}y + \frac{1}{2}y^2 + yz|_0^1 dz = \int_0^1 1 + z dz.$$
Now, we evaluate the remaining integral to obtain
$$z + \frac{1}{2}z^2|_0^1 = \frac{3}{2}.$$
Our next example uses integration by parts. This technique is covered in depth in the article Integration by Parts Explained with Examples: A Step-by-Step Guide. In applying this method, we will need to take a partial derivative. Partial differentiation is covered in The Ultimate Beginner’s Guide to Partial Derivatives with Step-by-Step Examples.
Example 4: Evaluate \( \int_0^1 \int_0^1 \int_0^x xze^y dydxdz \).
Solution: The inner integral is with respect to y, so we treat \( x \) and \( z \) as constants and integrate with respect to \( y \) to get
$$\int_0^1 \int_0^1 xze^y|_0^x dxdz = \int_0^1 \int_0^1 xze^x – xz dxdz.$$
We now integrate with respect to x while treating z as a constant. We begin by using linearity, which gives
$$\int_0^1 \int_0^1 xze^x dx – \int_0^1 xz dx dz.$$
The first integral can be evaluated using integration by parts. Choose \( u = xz \) and \( dv = e^xdx \), then \( du = zdx \) and \( v = e^x \). Applying the integration by parts formula to the first integral then gives
$$\int_0^1 xze^x|_0^1 – \int_0^1 ze^x dx – \int_0^1 xz dx dz = \int_0^1 ez – ze^x|_0^1 – \frac{1}{2}x^2z|_0^1 dz = \int_0^1 \frac{1}{2}z dz.$$
Now, we evaluate the remaining integral to obtain
$$\frac{1}{4}z^2|_0^1 = \frac{1}{4}.$$
Our last example involves trigonometric functions and uses the techniques covered in the guide How to Integrate Products of Trigonometric Functions: Techniques and Tricks.
Example 5: Evaluate \( \int_0^1 \int_0^{\frac{\pi}{2}} \int_0^y \cos(y)\sin(z) dzdydx \).
Solution: The inner integral is with respect to z, so we treat \( x \) and \( y \) as constants and integrate with respect to \( z \) to get
$$ – \int_0^1 \int_0^{\frac{\pi}{2}} \cos(y)\cos(z)|_0^y dydx = – \int_0^1 \int_0^{\frac{\pi}{2}} \cos^2(y) – \cos{y} dydx.$$
We now integrate with respect to y while treating x as a constant. We begin by applying the power-reducing identity for cosine, which gives
$$- \int_0^1 \int_0^{\frac{\pi}{2}} \frac{1}{2} + \frac{1}{2}\cos(2y) – \cos{y} dydx = – \int_0^1 \frac{1}{2}y + \frac{1}{4}\sin(2y) – \sin{y}|_0^{\frac{\pi}{2}} dx = – \int_0^1 \frac{\pi}{4} – 1 dx.$$
Now, we evaluate the remaining integral to obtain
$$-(\frac{\pi}{4} – 1)x|_0^1 = 1 – \frac{\pi}{4}.$$
Conclusion
In this guide, we explored the fundamental techniques for evaluating double and triple integrals over general regions. The key to effectively solving these problems lies in visualizing the region of integration and setting up the limits correctly. Once the bounds are established, the remaining integration steps follow from familiar single-variable calculus techniques. As you continue to practice, you’ll build the intuition needed to handle more complex regions.