Differentiation Infographic

Related Article:

How to Differentiate a Function Step by Step: A Beginner’s Guide

Related Videos:

How to Differentiate Any Function Using These 3 Rules

Product Rule for Beginners

How to Use the Quotient Rule

Chain Rule for Beginners

Learn Implicit Differentiation Fast with This Example

Logarithmic Differentiation Explained Step by Step

Master Higher-Order Derivatives

Notes:

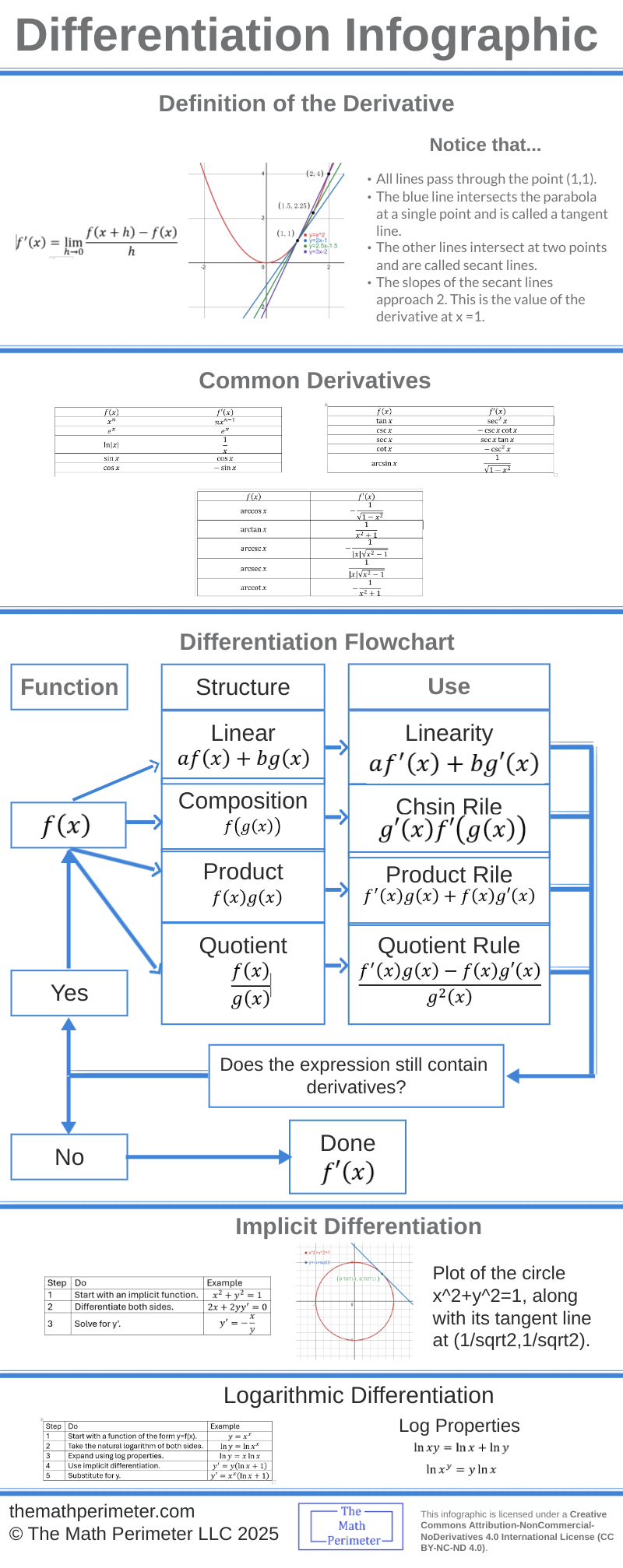
The constant rule is not included in this infographic. However, the constant rule can be derived from the power rule:

$$\frac{d}{dx}C = \frac{d}{dx}Cx^0 = C \cdot 0x^{-1} = 0.$$.

The constant multiple and sum and difference rules are not included, but linearity combines these two rules. In terms of differentiation, linearity involves the two criteria:

$$\frac{d}{dx}(cf(x) = c\frac{d}{dx}f(x)$$
$$\frac{d}{dx}(f(x) + g(x)) = \frac{d}{dx}f(x) + \frac{d}{dx}.g(x).$$

In the infographic, we combine these into the equivalent criterion

$$\frac{d}{dx}(af(x) + bg(x)) = a\frac{d}{dx}f(x) + b\frac{d}{dx}g(x).$$

As an example of using the flow chart to compute derivatives, let’s calculate (\((\sin{x} + \cos{x})^2)’\). We have a composition, so we use the chain rule, which gives \(2(\sin{x} + \cos{x})(\sin{x} + \cos{x})’\). Our expression still contains a derivative, so we continue the process. This time we have a linear function, so we apply linearity, arriving at \(2(\sin{x} + \cos{x})(\cos{x} – \sin{x})\). There are no more derivatives, so we are done.

License:

This differentiation infographic is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike license. That means you’re free to share, modify, and distribute the infographic if you provide proper attribution, don’t use it for commercial purposes, and derivative works are licensed under compatible terms.

If your intended use falls outside these rights, please contact me at
legal@themathperimeter.com. We can make arrangements for proper licensing.