If you’re studying multivariable calculus for the first time, chances are you’ve encountered the concept of partial derivatives. This beginner’s guide to partial derivatives offers explanations and examples to help you understand what partial derivatives are and how they work.
Partial derivatives are an extension of ordinary derivatives from single-variable calculus. However, instead of analyzing how a function changes with respect to just one variable, partial derivatives let you explore how a multivariate function changes with respect to one variable while keeping the others fixed.
In this guide, we’ll cover the basic definition of a partial derivative, as well as more advanced topics like the multivariable chain rule, differentials, implicit differentiation, and higher-order partial derivatives. Each concept is introduced with detailed explanations, followed by one or more examples.
To learn about partial derivatives, you must first understand ordinary derivatives. If you haven’t already, please refer to the article How to Differentiate a Function Step by Step: A Beginner’s Guide to learn about derivatives of single variable functions.
For a visual approach to learning this topic, please refer to my Partial Derivatives Infographic.
What Is a Partial Derivative?
A partial derivative measures how a multivariable function changes as one of its variables changes while all other variables are held constant.
Notation
The most common notations for partial derivatives are:
\( \frac{\partial f}{\partial x} \): the partial derivative of \( f \) with respect to \( x \).
\( \frac{\partial f}{\partial y} \): the partial derivative of \( f \) with respect to \( y \).
\( f_x \): shorthand for \( \frac{\partial f}{\partial x} \).
\( f_y \): shorthand for \( \frac{\partial f}{\partial y} \).
Examples
Example 1: Find all partial derivatives of \( f(x, y) = x^2y + y^3 \).
Solution: To find \( \frac{\partial f}{\partial x} \) we treat \( y \) as a constant and differentiate with respect to x using the power rule to obtain
$$f_x = 2xy.$$
Similarly, To find \( \frac{\partial f}{\partial y} \), we treat \( x \) as a constant and differentiate with respect to y to get
$$f_y = x^2 + 3y^2.$$
Example 2: Find all partial derivatives of \( f(x, y) = e^{x^2 + y^2} \).
Solution: To find \( \frac{\partial f}{\partial x} \) we treat \( y \) as a constant and differentiate with respect to x using the chain rule to obtain
$$f_x = 2x e^{x^2 + y^2}.$$
Similarly, to find \( \frac{\partial f}{\partial y} \), we treat \( x \) as a constant and differentiate with respect to y to get
$$f_y = 2y e^{x^2 + y^2}.$$
Example 3: Find all partial derivatives of \( f(x, y) = x \sin(x^2 + y^2) \).
Solution: To find \( \frac{\partial f}{\partial x} \), we treat \( y \) as a constant and differentiate with respect to x using the product and chain rules to obtain
$$f_x = \sin(x^2 + y^2) + 2x^2 \cos(x^2 + y^2).$$
Similarly, to find \( \frac{\partial f}{\partial y} \), we treat \( x \) as a constant and differentiate with respect to y using the chain rule to get
$$f_y = 2xy \cos(x^2 + y^2).$$
Example 4: Find all partial derivatives of \( f(x, y) = \frac{x}{x + y} \).
Solution: To find \( \frac{\partial f}{\partial x} \), we treat \( y \) as a constant and differentiate with respect to x using the quotient rule to obtain
$$f_x = \frac{y}{(x + y)^2}.$$
To differentiate, with respect to y, we first rewrite the function using exponent rules, which gives
$$f(x, y) = x(x + y)^{-1}.$$
To find \( \frac{\partial f}{\partial y} \), we treat \( x \) as a constant and differentiate with respect to y using the chain rule to get
$$f_y = – x(x + y)^{-2} = -\frac{x}{(x + y)^2}.$$
Higher Order Partial Derivatives
Just like you can take higher-order ordinary derivatives in single-variable calculus, you can also take higher-order partial derivatives. A higher-order partial derivative means taking a partial derivative more than once. The notation for second order partial derivatives is \( \frac{\partial^2 f}{\partial x^2} \), \( \frac{\partial^2 f}{\partial y^2} \), \( \frac{\partial^2 f}{\partial y \partial x} \), and \( \frac{\partial^2 f}{\partial x \partial y} \). Respectively, these are also denoted \( f_{xx} \), \( f_{yy} \), \( f_{xy} \), and \( f_{yx} \).
As long as the mixed partial derivatives are continuous, then the order of differentiation doesn’t matter, and
$$\frac{\partial^2 f}{\partial x \partial y} = \frac{\partial^2 f}{\partial y \partial x}.$$
Example 5: Find all second-order partial derivatives of \( f(x, y) = x^2y + y^3 \).
Solution: First, recall from Example 1 that the first-order partial derivatives are:
$$f_x = 2xy,$$
$$f_y = x^2 + 3y^2.$$
The second-order partial derivatives are then:
$$f_{xx} = (f_x)_x = (2xy)_x =2y,$$
$$f_{xy} = (f_x)_y = (2xy)_y = 2x,$$
$$f_{yx} = (f_y)_x = (x^2 + 3y^2)_x = 2x,$$
$$f_{yy} = (f_y)_y = (x^2 + 3y^2)_y = 6y.$$
Notice that \( f_{xy} = f_{yx} = 2x \).
Implicit Differentiation with Partial Derivatives
Sometimes, a function is not given explicitly in terms of one variable. Instead, you’re given an equation involving multiple variables, and you want to find how one variable changes with respect to another. This is where implicit differentiation comes in. It allows you to find derivatives of implicitly defined functions even when you can’t solve explicitly for a given variable.
Suppose \( F(x, y, z) = 0 \), then
$$\frac{\partial z}{\partial x} = -\frac{F_x}{F_z},$$
and
$$\frac{\partial z}{\partial y} = -\frac{F_y}{F_z}.$$
Examples
Example 6: Given \( x^2 + y^2 + z^2 = 1 \), compute \( \frac{\partial z}{\partial x} \) and \( \frac{\partial z}{\partial y} \).
Solution: Subtracting 1 from both sides of the equation gives
$$x^2 + y^2 + z^2 – 1 = 0.$$
Applying the formulas, we obtain
$$\frac{\partial z}{\partial x} = -\frac{( x^2 + y^2 + z^2 – 1)_x}{(x^2 + y^2 + z^2 – 1)_z} = -\frac{2x}{2z} = -\frac{x}{z}$$
$$\frac{\partial z}{\partial y} = -\frac{(x^2 + y^2 + z^2 – 1)_y}{(x^2 + y^2 + z^2 – 1)_z} = -\frac{2y}{2z} = -\frac{y}{z}.$$
Example 7: Given \( xyz = 1 \), compute \( \frac{\partial z}{\partial x} \) and \( \frac{\partial z}{\partial y} \).
Solution: Subtracting 1 from both sides of the equation gives
$$xyz – 1 = 0.$$
Applying the formulas, we obtain
$$\frac{\partial z}{\partial x} = -\frac{(xyz – 1)_x}{(xyz – 1)_z} = -\frac{yz}{xy} = -\frac{z}{x}$$
$$\frac{\partial z}{\partial y} = -\frac{(xyz – 1)_y}{(xyz – 1)_z} = -\frac{xz}{xy} = -\frac{z}{y}.$$
The Chain Rule for Partial Derivatives
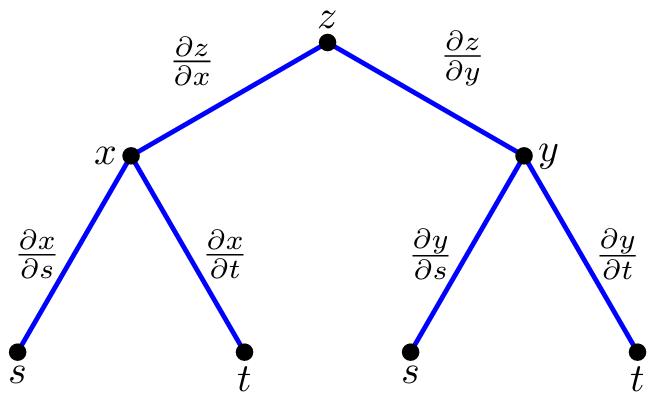
In multivariable calculus, the chain rule allows you to compute derivatives of composite functions. If a variable depends on intermediate variables, and those variables depend on others, you can use a tree diagram to organize the dependencies and compute the derivative. For example, suppose a variable \( z \) depends on \( x \) and \( y \), and \( x \) and \( y \) depend on \( s \) and \( t \).
The Chain Rule Formulas and Tree Diagrams
Suppose \( z = f(x(s, t), y(s, t)) \), then the chain rule says
$$\frac{\partial z}{\partial s} = \frac{\partial z}{\partial x} \cdot \frac{\partial x}{\partial s} + \frac{\partial z}{\partial y} \cdot \frac{\partial y}{\partial s},$$
and
$$\frac{\partial z}{\partial t} = \frac{\partial z}{\partial x} \cdot \frac{\partial x}{\partial t} + \frac{\partial z}{\partial y} \cdot \frac{\partial y}{\partial t}.$$
You can visualize this with the tree diagram:
Examples
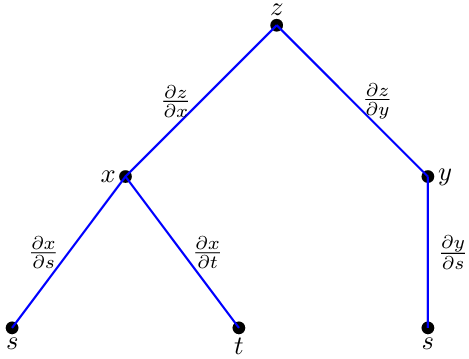
Example 8: Given \( z = x^2 y + y^2 \), compute \( \frac{\partial z}{\partial s} \) and \( \frac{\partial z}{\partial t} \), where \( x = s + t \) and \( y = s – t \).
Solution: The tree diagram for this situation is
The chain rule then states that
$$\frac{\partial z}{\partial s} = \frac{\partial z}{\partial x} \cdot \frac{\partial x}{\partial s} + \frac{\partial z}{\partial y} \cdot \frac{\partial y}{\partial s}$$
$$\frac{\partial z}{\partial t} = \frac{\partial z}{\partial x} \cdot \frac{\partial x}{\partial t} + \frac{\partial z}{\partial y} \cdot \frac{\partial y}{\partial t}.$$
Plugging everything into the formulas gives
$$\frac{\partial z}{\partial s} = \frac{\partial}{\partial x}( x^2 y + y^2) \cdot \frac{\partial}{\partial s}(s + t) + \frac{\partial}{\partial y}(x^2 y + y^2) \cdot \frac{\partial}{\partial s}(s – t) = 2xy + x^2 + 2y$$
$$\frac{\partial z}{\partial t} = \frac{\partial}{\partial x}( x^2 y + y^2) \cdot \frac{\partial}{\partial t}(s + t) + \frac{\partial}{\partial y}(x^2 y + y^2) \cdot \frac{\partial}{\partial t}(s – t) = 2xy – x^2 – 2y$$
Example 9: Given \( z = \sin(xy) \), compute \( \frac{\partial z}{\partial x} \) and \( \frac{\partial z}{\partial y} \), where \( x = st \) and \( y = s^2 \).
Solution: The tree diagram for this situation is
The chain rule then states that
$$\frac{\partial z}{\partial s} = \frac{\partial z}{\partial x} \cdot \frac{\partial x}{\partial s} + \frac{\partial z}{\partial y} \cdot \frac{\partial y}{\partial s}$$
$$\frac{\partial z}{\partial t} = \frac{\partial z}{\partial x} \cdot \frac{\partial x}{\partial t}.$$
Plugging everything into the formulas gives
$$\frac{\partial z}{\partial s} = \frac{\partial}{\partial x}(\sin(xy)) \cdot \frac{\partial}{\partial s}(st) + \frac{\partial}{\partial y}(\sin(xy)) \cdot \frac{\partial}{\partial s}(s^2) = ty\cos(xy) + 2sx\cos(xy)$$
$$\frac{\partial z}{\partial t} = \frac{\partial}{\partial x}(\sin(xy)) \cdot \frac{\partial}{\partial t}(st) = sy\cos(xy).$$
Differentials
In single-variable calculus, you learned that the differential of a function \( y = f(x) \) is given by
$$dy = f'(x) \, dx.$$
Differentials generalize to functions of several variables. If \( z = f(x, y) \), the differential \( dz \) is given by
$$dz = \frac{\partial z}{\partial x} \, dx + \frac{\partial z}{\partial y} \, dy.$$
Example 10: Find the differential \( dz \) for \( z = x^2 y + y^3 \).
Solution: Plugging the function into the formula gives us
$$dz = \frac{\partial}{\partial x}( x^2 y + y^3 ) \, dx + \frac{\partial}{\partial y}(x^2 y + y^3) \, dy = 2xydx + (x^2 + 3y^2)dy.$$
Conclusion
Understanding partial derivatives is an important step for anyone studying multivariable calculus. In this guide, you learned how to compute partial derivatives of multivariable functions, apply the chain rule to multivariate functions, compute differentials, use implicit differentiation, and calculate higher-order partial derivatives. These techniques will be helpful as you continue your mathematical journey.