Not all integrals are straightforward; some require advanced algebraic techniques to rewrite expressions before integration. One such method is completing the square, an algebraic tool that transforms quadratic expressions into a more manageable form. In this guide on how to solve integrals by completing the square, we’ll take you step by step through how to solve integrals using this technique.
This article is part of a three-part series on integrals of rational functions. To learn this topic visually, please refer to the Integrating Rational Functions Infographic.
Completing the Square
Before applying this technique to integration, it’s necessary to understand what completing the square means. Given a quadratic expression:
$$ax^2 + bx + c.$$
We can rewrite it in the form:
$$a(x – h)^2 + k.$$
where \( h = -\frac{b}{2a} \) and \( k = c – \frac{b^2}{4a} \).
Now, let’s see how this technique is used in integration.
When to Use Completing the Square in Integration
Completing the square is particularly useful when dealing with integrals involving rational functions or square roots, such as:
Irreducible quadratic under square roots:
$$\int \sqrt{ax^2 + bx + c} dx.$$
Irreducible quadratics in the denominator:
$$\int \frac{1}{ax^2 + bx + c} dx.$$
This transformation takes integrals containing an irreducible quadratic to an integral that can be solved via the substitution rule or trigonometric substitution.
Steps to Solving Integrals by Completing the Square
Step 1: Recognizing the Need for Completing the Square
Completing the square is often the best approach if the integral involves an irreducible quadratic in the denominator or under a square root.
Step 2: Completing the Square
As an example, we complete the square for the quadratic \( 2x^2 + 12x + 16 \). We start by factoring out a 2 to get \( 2(x^2 + 6x + 8) \). \( \frac{6}{2}^2 = 3^2 = 9 \), so we rewrite the quadratic as $$2(x^2 + 6x + 9 – 1) = 2((x + 3)^2 – 1)) = 2(x + 3)^2 – 2.$$
Step 3: Using a Substitution.
Perform the substitution \( u = x – h \). If you need help with the substitution, check out The Ultimate Step-by-Step Guide to Solving Integrals Using Substitution.
Step 4: Solving the Integral
Solve the resulting integral via other methods. Don’t forget to back substitute.
Worked Out Examples
This first example demonstrates how the process works.
Example 1: Evaluate \( \int \frac{1}{x^2 + 6x + 10} dx \).
Solution: First, we complete the square to obtain
$$\int \frac{1}{x^2 + 6x + 10} dx = \int \frac{1}{x^2 + 6x + 9 + 1} dx = \int \frac{1}{(x + 3)^2 + 1} dx.$$
Let \( u = x + 3 \), then \( du = dx \). Substituting into the integral, we arrive at
$$\int \frac{1}{u^2 + 1} dx = \arctan{u} + C = \arctan{(x + 3)} + C.$$
Trigonometric substitution is often needed when completing the square to solve integrals. It will be needed in the following examples. If you haven’t already, please refer to my guide, Trigonometric Substitution for Beginners: A Step-by-Step Guide.
Example 2: Evaluate \( \int \frac{1}{\sqrt{x^2 + 4x + 5}} dx \).
Solution: First, we complete the square to obtain
$$\int \frac{1}{\sqrt{x^2 + 4x + 5}} dx = \int \frac{1}{\sqrt{x^2 + 4x + 4 + 1}} dx = \int \frac{1}{\sqrt{(x + 2)^2 + 1}} dx.$$
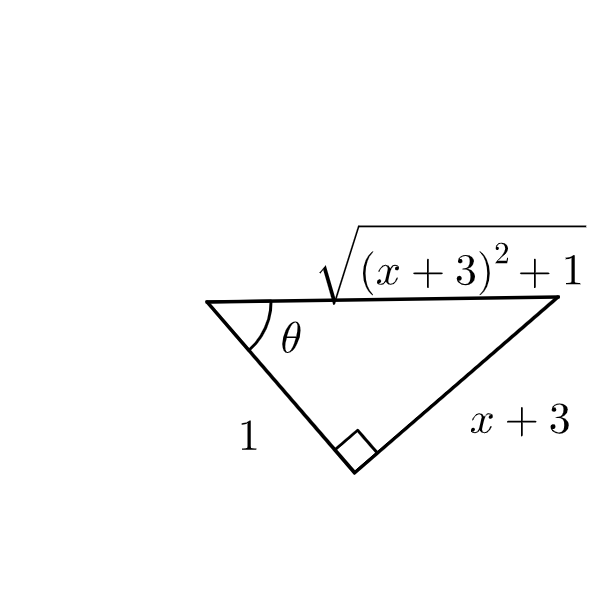
Let \( x + 2 = \tan{\theta} \), then \( dx = \sec^2{\theta} d\theta \). Substituting into the integral, we arrive at
$$\int \frac{1}{\sqrt{\tan^2{\theta} + 1}}\sec^2{\theta} d\theta = \int \frac{1}{\sqrt{\sec^2{\theta}}}\sec^2{\theta} d\theta = \int \frac{1}{\sec{\theta}}\sec^2{\theta} d\theta = \int \sec{\theta} d\theta = \int \frac{\sec{\theta}(\sec{\theta} + \tan{\theta})}{\sec{\theta} + \tan{\theta}} d\theta = \int \frac{\sec^2{\theta} + \sec{\theta}\tan{\theta}}{\sec{\theta} + \tan{\theta}} d\theta. $$
Let \( u = \sec{\theta} + \tan{\theta} \), then \( du = \sec^2{\theta} + \sec{\theta}\tan{\theta} d\theta \). Substituting into the integral, we get
$$ \int \frac{1}{u} du = \ln{|u|} + C = \ln{|\sec{\theta} + \tan{\theta}|} + C. $$
Using the triangle to convert everything back into terms of x, we arrive at
$$ \ln{|x + 3 + \sqrt{(x + 3)^2 + 1}|} + C = \ln{|x + 3 + \sqrt{x^2 + 6x + 10}|} + C. $$
Our last example is the most difficult. It uses all the methods discussed in this article and Basic Integration Problems for Beginners.
Example 3: Evaluate \( \int \frac{2x + 7}{(x^2 + 6x + 10)^2} dx \).
Solution: We first use linearity to split the integral into two integrals as follows:
$$\int \frac{2x + 6}{(x^2 + 6x + 10)^2} dx + \int \frac{1}{(x^2 + 6x + 10)^2} dx.$$
Now, we complete the square in the second integral, which gives
$$\int \frac{2x + 6}{(x^2 + 6x + 10)^2} dx + \int \frac{1}{(x^2 + 6x + 9 + 1)^2} dx = \int \frac{2x + 6}{(x^2 + 6x + 10)^2} dx + \int \frac{1}{((x + 3)^2 + 1)^2} dx.$$
In the first integral, let \( u = x^2 + 6x + 10 \), then \( du = (2x + 6)dx \). For the second integral, let \( x + 3 = \tan{\theta} \), then \( dx = \sec^2{\theta} d\theta \). Substituting into the integral, we have
$$\int \frac{1}{u^2} du + \int \frac{1}{(\tan^2{\theta}+ 1)^2}\sec^2{\theta} d\theta = \int \frac{1}{u^2} du + \int \frac{1}{(\sec^2{\theta})^2}\sec^2{\theta} d\theta = \int \frac{1}{u^2} du + \int \frac{1}{\sec^2{\theta}} d\theta = \int u^{-2} du + \int \cos^2{\theta} d\theta.$$
Applying the power reducing identity, we get
$$\int u^{-2} du + \int \frac{1}{2} + \frac{1}{2}\cos{2\theta} d\theta = -u^{-1} + \frac{1}{2}\theta + \frac{1}{4}\sin{2\theta} + C = -\frac{1}{u} + \frac{1}{2}\theta + \frac{1}{2}\sin{\theta}\cos{\theta} + C.$$
Using the triangle and back substituting gives us
$$-\frac{1}{x^2 + 6x + 10} + \frac{1}{2}\arctan{(x + 3)} + \frac{1}{2}\frac{x + 3}{(x + 3)^2 + 1} + C = \frac{x + 1}{2(x^2 + 6x + 10)} + \frac{1}{2}\arctan{(x + 3)} + C.$$
Conclusion
Completing the square is an integration technique used when dealing with irreducible quadratics. By transforming the integral into a simpler form, you can apply standard integration techniques like u-substitution or trigonometric substitution. With practice, you’ll master using this method.